令和2年2月19日(水)講座14「続々・サイエンス教室〜身近な電子機器と数のはなし〜」の第2回「おもしろ数学のはなし」を花川北コミュニティセンターで行いました。講師は元北海道大学教授の三島瑛人さん、受講者は32名でした。

2月5日(水)の第1回に引き続き、今回は数学についてお話しいただきました。数学は専門ではなく使っていただけですと断って話を始められましたが、三島さんは札幌のカルチャーセンターで高校と大学の数学を教えておられますので的確でおもしろい話をしていただいたと思っています。以下にその概要を紹介致します。

1.単位のあるものの四則演算のはなし
・リンゴ1個とリンゴ1個で2個になりますが、リンゴ1個とカキ1個で2個になると考えられるでしょうか?果物1個と果物1個では果物2個になり、純粋な数学では1+1=2となります。すなわち、同じとみなせないと足し算はできず、同じとみなせると足し算ができるのです。引き算でも同じことで、同種のものどうしは結びつけることができます(下図)。

・掛け算と割り算ではどうでしょうか。3個入りの箱、2箱では6個となります(純粋数学では3×2=6となる)。6個を3個入りの箱に分けると2箱になります(純粋数学では6÷3=2)。掛け算と割り算は基本的に違うものどうしを結びつけます。
・「100キロを50キロで走ると2時間で着く」を「100キロ÷50キロ=2時間」と書くと、単位まで考えた場合誤りになります。単位を考えると「100キロを時速50キロで走ると2時間で着く」となり、「100km÷50km/時間=2時間」と書くべきです。
2.単位のはなし
・基本単位〜長さの単位(m[メートル、メーター])、時間の単位(s[秒])、質量の単位(g[グラム])などがあります。
・接頭辞〜大きい方へは、k(キロ[103];kは小文字)、M(メガ[106])、G(ギガ[109])T(テラ[1012])、P(ペタ[1015])があります。一方、小さい方へは、m(ミリ[10-3])、μ(マイクロ[10-6])、n(ナノ[10-9])、p(ピコ[10-12])、f(ヘムト[10-15])などがあります。他にも、ヘクトパスカルやヘクトアールなどのh(ヘクト[100])、およびc(センチ[100分の1])やd(デシ[10分の1])なども使われています。
・情報の単位〜bit(ビット)やB(バイト)などがあります。bit(ビット)は「白」か「黒」か、「0」か「1」か、「ある」か「ない」かなどの単位です。B(バイト)は8ビットのことで、英字・数字は8bitで1文字を表すのでよく使われます。日本語の場合は漢字があるので2B(=16bit)で1文字を表します。
・通信速度の単位〜bps(ビー・ピー・エス[bit per second])があり、1秒間に1ビットの速度を表します。例えば、10Mbps(10メガbps)の通信速度とは1秒間に10×106bit=8×1,250,000bit、つまり1秒間に125万文字の英数字を送る速度です。日本語の場合は2Bで1文字なので125万の半分となり、400字詰の原稿用紙であれば1秒間で約1,560枚の原稿を送る速度になります。
3.負の数の掛け算と累乗のはなし
・「負の数と負の数との掛け算はどうして正の数になるのか?」の疑問について考えます。下図左では、5×3=15から5×(-2)=-10まで5づつ減っています。一方、(-2)×3= -6から(-2)×(-2)=4までは2づつ増えています。結果として、(-2)×(-1)=2で、「負の数と負の数との掛け算で正の数になっている」のです(下図中)。
・累乗では下図右のように、32=9から3-2=1/9までが1/3づつ減っています。

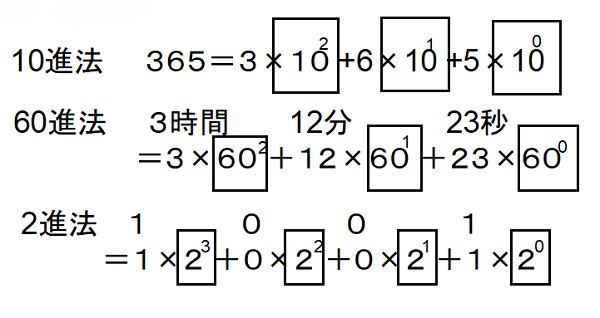
4.10進法、60進法、2進法のはなし
・下図のように、10進法では3桁目が102、2桁目が101、1桁目が100となり、累乗部分(上付き文字のところ)が1づつ減っています。同様に、60進法の3時間12分23秒でも累乗部分が1づつ減っています。コンピューターの内部では2進法を使っていますが2進法でも同様です。
・2進数を10進数と比較して表したのが下図です。2進数では0と1だけを使い"2"は使えないので、10進数の「2」は「10」となります。一つ玉の算盤を考えるとよく分かります。なお、2進数は(101)2のように下付き文字の2を添えて表すことがあります。10進数での5を2進数で書くと101になり、3桁目が22、2桁目が21、1桁目が20となる様子が下図に示されています。


・2進法による掛け算として6×5=30の例が下図に示されています。

5.対数のはなし
・下図上の性質を利用すると、掛け算が足し算に、割り算が引き算になります。これは対数につながり、計算尺は対数を利用した掛け算機ととらえることができます。対数(ロガリズム)」の定義によると、y=10xの場合、これをx=log yと表します(下図下)。対数表を使えば、log 2=0.3010‥が直ぐ出てきます。


・ 対数を使った簡単な計算例を以下に示します。対数および対数表を使えば掛け算を足し算だけで計算することができます。

6.集団の表し方のはなし
・以下のような点数だけでは集団全体の傾向をとらえることができません。
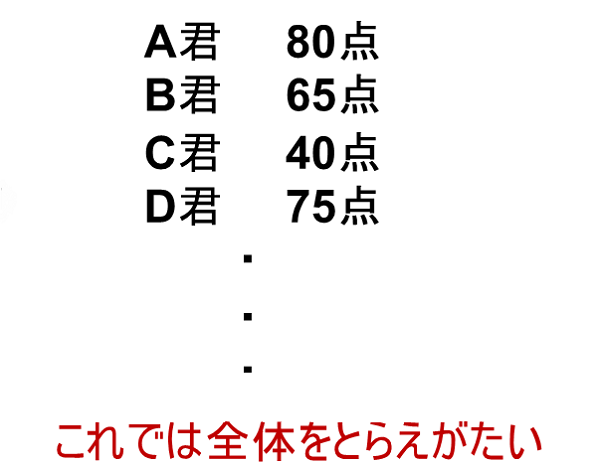
・10点刻みで人数を示すか、グラフで示したりすると少しは全体像を見ることができます。
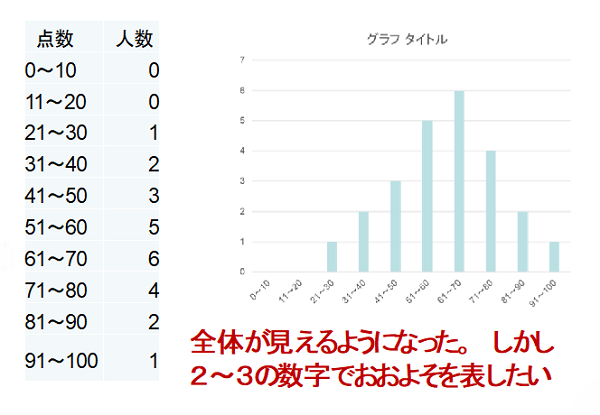
・分散、標準偏差、偏差値の考えを導入すると、さらに全体像をとらえることができます。それぞれの定義は以下の通りです(下図上)。4人の点数分布をもった2組の例を以下に示します(下図下)。2組とも平均点は60点で同じですが、標準偏差(σ)では10と20になり、下の組の方がばらつき大となっています。


・50人のクラスの点数を正規分布を仮定して表したのが下のグラフです。これから、偏差値(SS)、5段階評価と人数分布などが分かります。集団を表す数値では平均値の次に標準偏差が大事です。
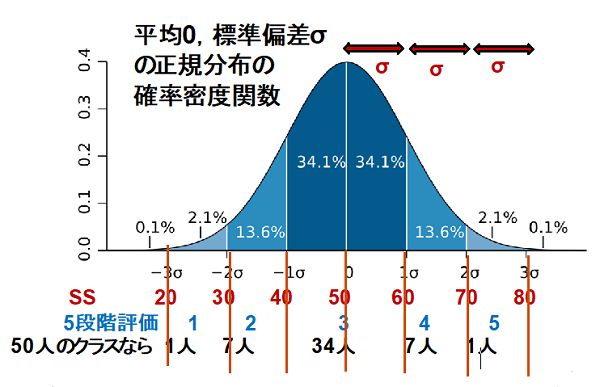
7.等号の考え方(移項)のはなし
・等号と移項をどのように考えるか、以下の図に示します。等号は天秤を考えると分かりやすくなります。

最後に受講者から寄せられた感想をいくつか紹介します。
「何年ぶりかで数学の話を聞いて新鮮でした。数学は難しい」
「大変勉強になりました。特に、標準偏差の考え方、出し方など、これまで良くわかっていなかったが、よく分かりました」
「ちょっと難しかったですが、とてもおもしろかったです。学生時代を思い出しましたが、今はまったく使わなくなりましたね〜 PCを使っていろいろやって見ます」
「全体に難しい。対数表はなつかしい書類でした。計算機のない頃、この表を図書室で引いて使用した記憶がある」
「単位のお話はわかり易く、通信機器の契約とか、精度とかが理解できます。対数の内容にはついていけませんでした。集団の表し方は数学を使って多面から分析できそうで、おもしろかったです。移項にしても、機械的にやり方だけ知っていただけでしたが、意味があることも知りました。お話し、有り難うございました」
「半世紀以上前、PCや電子計算機もない時代、手回し計算機や計算尺・対数表で算出していた若き日を想い、久しぶりに熱くなってきた」
「身近な電子機器と数の話、三島講師により基礎計算法を教わり、私共が日頃感じなかった専門的な考え、計算のことなどを学び、大変参考になりました。おもしろかったですよ。色々と幅広く学びを教えて下さり、お礼申し上げます」
「もう少しレベルを下げてほしかった。偏差値や移行のところがやや面白かったが」
















